13597. Точки L
, A
и T
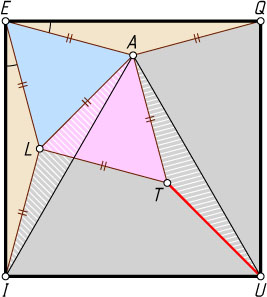
расположены внутри квадрата EQUI
, причём EQA
и EIL
— равнобедренные треугольники с основаниями EQ
и EI
соответственно, а EAL
и ALT
— равносторонние. Докажите, что UT=IL
.
Решение. Поскольку LI=LE=AE=AQ
, треугольники ELI
и EAQ
равны по трём сторонам. Значит, углы при их основаниях равны, а так как их сумма равна 30^{\circ}
, то каждый из них равен 15^{\circ}
.
Для доказательства равенства UT=IL
достаточно доказать равенство треугольников ALI
и ATU
.
Поскольку
AL=EL~\mbox{и}~\angle ALI=360^{\circ}-\angle ELI-\angle ALE=
=360^{\circ}-150^{\circ}-60^{\circ}=150^{\circ}=\angle ELI,
то треугольники ALI
и ELI
равны по двум сторонам и углу между ними, поэтому AI=EI=IU
, т. е. треугольник AIU
равнобедренный. Кроме того,
\angle AIU=90^{\circ}-\angle LIE-\angle LIA=90^{\circ}-2\cdot15^{\circ}=60^{\circ},
значит, этот треугольник равносторонний. Тогда AU=AI
. Наконец,
\angle TAU=\angle UAI-\angle TAI=60^{\circ}-\angle TAI=\angle TAL-\angle TAI=\angle LAI.
Таким образом треугольники ALI
и ATU
равны по двум сторонам и углу между ними. Следовательно, UT=IL
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1997, № 8, задача H215, с. 494
