1360. Внутри угла с вершиной O
взята некоторая точка M
. Луч OM
образует со сторонами угла углы, один из которого больше другого на 10^{\circ}
; A
и B
— проекции точки M
на стороны угла. Найдите угол между прямыми AB
и OM
.
Ответ. 80^{\circ}
.
Указание. Точки A
, O
, B
и M
лежат на одной окружности.
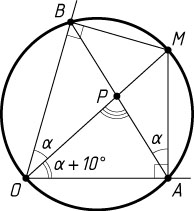
Решение. Пусть
\angle BOM=\alpha,~\angle AOM=\alpha+10^{\circ},
P
— точка пересечения прямых AB
и OM
.
Поскольку отрезок OM
виден из точек A
и B
под прямым углом, то точки A
и B
лежат на окружности с диаметром OM
, а APO
— внешний угол треугольника APM
. Следовательно,
\angle APO=\angle AMO+\angle BAM=
=(90^{\circ}-\angle AOM)+\angle BOM=90^{\circ}-(\alpha+10^{\circ})+\alpha=80^{\circ}
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 65, с. 165
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.16, с. 104
