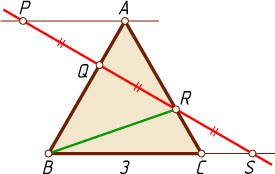
13625. Через вершину A
равностороннего треугольника ABC
со стороной 3 проведена прямая, параллельная BC
(см. рис.). Через точку P
, лежащую на этой прямой, проведена прямая, пересекающая стороны AB
, AC
и прямую BC
в точках Q
, R
и S
соответственно, причём PQ=QR=RS
. Найдите BR
.
Ответ. \sqrt{7}
.
Решение. Треугольник PRA
подобен треугольнику SRC
с коэффициентом \frac{PR}{SR}=2
, поэтому AR=2RC
. Значит, RC=\frac{1}{3}AC=1
.
Следовательно, по теореме косинусов
BR=\sqrt{CB^{2}+CR^{2}-2CB\cdot CR\cos60^{\circ}}=\sqrt{9+1-2\cdot3\cdot1\cdot\frac{1}{2}}=
=\sqrt{9+1-3}=\sqrt{7}.
Источник: Журнал «Crux Mathematicorum». — 1999, № 4, задача 12, с. 219
Источник: Канадские математические олимпиады. — 1993
