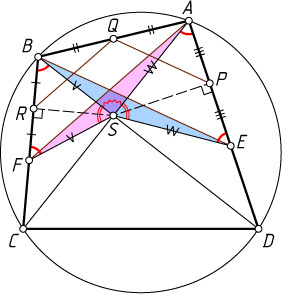
13627. Точка Q
— середина стороны AB
вписанного четырёхугольника ABCD
, диагонали которого пересекаются в точке S
. Точки P
и R
— проекции точки S
на стороны AD
и BC
соответственно. Докажите, что PQ=QR
.
Решение. Пусть E
и F
— точки, симметричные точкам A
и B
относительно P
и R
соответственно. Треугольники ASE
и BSF
равнобедренные, SE=SA
и SF=SB
, а четырёхугольник ABCD
вписанный, поэтому
\angle AES=\angle EAS=\angle DAC=\angle DBC=\angle SBF=\angle BFS.
Значит, равны углы ASE
и BSF
при вершинах равнобедренных треугольников ASE
и BSF
. Тогда
\angle BSE=\angle BSA+\angle ASE=\angle BSA+\angle BSF=\angle FSA.
Следовательно, треугольники SEB
и SAF
равны по двум сторонам и углу между ними, поэтому BE=FA
.
Отрезки PQ
и QR
— средние линии треугольников ABE
и ABF
, следовательно,
PQ=\frac{1}{2}BE=\frac{1}{2}FA=QR.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1999, № 5, задача 4, с. 268
Источник: Словенские математические олимпиады. — 1998
