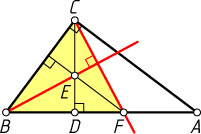
1363. В прямоугольном треугольнике ABC
к гипотенузе AB
проведена высота CD
. На отрезках CD
и DA
взяты точки E
и F
соответственно, причём \frac{CE}{CD}=\frac{AF}{AD}
. Докажите, что прямые BE
и CF
перпендикулярны.
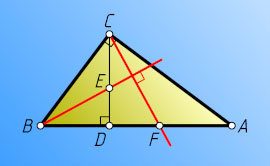
Указание. Высоты треугольника пересекаются в одной точке.
Решение. Из условия задачи следует, что \frac{DE}{DC}=\frac{DF}{DA}
, поэтому FE\parallel AC
. Значит, FE\perp BC
, и E
— точка пересечения высот треугольника BCF
. Следовательно, BE\perp CF
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 68, с. 165

