13653. На стороне AC
треугольника ABC
дана точка S
. Постройте прямую, проходящую через точку S
и пересекающую прямые BC
и AB
в точках P
и Q
соответственно так, что PQ=PA
.
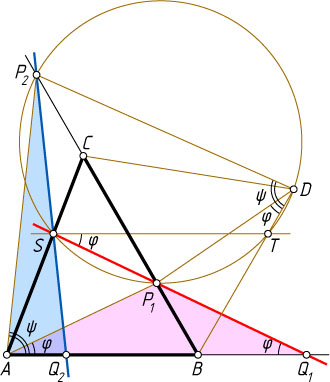
Решение. Пусть D
— точка, симметричная вершине A
относительно прямой BC
. Тогда треугольник DBC
равен треугольнику ABC
. Через точку S
параллельно AB
проведём прямую, пересекающую BD
в точке T
. Пусть описанная окружность треугольника STD
пересекает прямую BC
в точках P_{1}
и P_{2}
, а прямые SP_{1}
и SP_{2}
пересекают прямую AB
в точках Q_{1}
и Q_{2}
соответственно.
Докажем, что P_{1}Q_{1}=P_{1}A
и P_{2}Q_{2}=P_{2}A
.
Обозначим \angle P_{1}DT=\varphi
. Заметим, что прямая BC
— ось симметрии четырёхугольников ABDC
, ABDP_{1}
и ABDP_{2}
, а так как четырёхугольник SP_{1}TD
вписанный, то
\angle P_{1}ST=\angle P_{1}DT=\varphi.
Значит,
\angle P_{1}AB=\angle P_{1}DB=\varphi,
а так как ST\parallel AB
, то
\angle P_{1}Q_{1}A=\angle P_{1}ST=\varphi.
Значит, треугольник AP_{1}Q_{1}
равнобедренный. Следовательно, P_{1}Q_{1}=P_{1}A
.
Обозначим \angle P_{2}AQ_{2}=\psi
. Из симметрии
\angle P_{2}DB=\angle P_{2}AB=\psi,
а так как ST\parallel AB
и четырёхугольник P_{2}STD
вписанный, то
\angle AQ_{2}P_{2}=180^{\circ}-\angle P_{2}Q_{2}B=180^{\circ}-\angle P_{2}ST=
=\angle P_{2}DT=\angle P_{2}DB=\angle P_{2}AB=\psi.
Значит, треугольник AP_{2}Q_{2}
равнобедренный. Следовательно, P_{2}Q_{2}=P_{2}A
.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2000, № 7, задача 2473 (1999, с. 368), с. 442
