13656. В выпуклом пятиугольнике ABCDE
равны стороны BC
, CD
и DE
, а каждая диагональ параллельна одной из сторон. Докажите, что пятиугольник правильный.
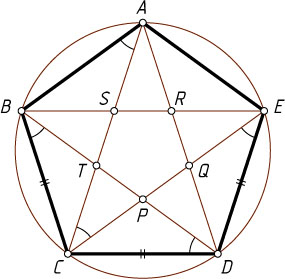
Решение. Пусть P
, Q
, R
, S
, T
— точки пересечения диагоналей (см. рис.). Четырёхугольник SCDE
— параллелограмм, так как BE\parallel CD
и AC\parallel ED
. Значит, CS=DE=CB
.
Поскольку BCDE
— равнобедренная трапеция, а AB\parallel CE
и BC\parallel AD
, то
\angle BAC=\angle ACE=\angle CED=\angle CBD=\angle BDC.
Значит, четырёхугольник ABCD
вписанный (как и BCDE
), и точки A
, B
, C
, D
и E
лежат на одной окружности, а так как хорды BC
и AD
этой окружности параллельны, то AB=CD
. Аналогично, AE=CD
. Таким образом, все стороны пятиугольника ABCDE
равны.
Кроме того, меньшие дуги AB
, BC
, CD
, DE
и EA
этой окружности равны, так как равны стягивающие их хорды. Обозначим \angle BAC=\alpha
. Тогда
\angle EAB=\angle ABC=\angle BCD=\angle CDE=\angle DEA=3\alpha.
Значит, все углы пятиугольника ABCDE
равны.
Итак, все стороны и все углы пятиугольника равны, следовательно, он правильный. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2000, № 8, задача 1 (1999, с. 74-75), с. 458
Источник: Австралийские математические олимпиады. — 1996
