13663. На боковой стороне AB
равнобедренного треугольника ABC
с основанием BC
и углом 20^{\circ}
при вершине A
отмечена точка P
, причём \angle BPC=30^{\circ}
. Докажите, что AP=BC
.
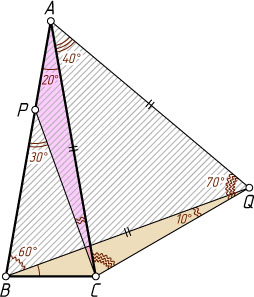
Решение. Построим вне треугольника ABC
равнобедренный треугольник ACQ
с основанием CQ
и углом 40^{\circ}
при вершине A
. Тогда треугольник ABQ
равносторонний, а по теореме о внешнем угле треугольника
\angle ACP=\angle BPC-\angle CAP=30^{\circ}-20^{\circ}=10^{\circ}.
Треугольники BCQ
и APC
равны по стороне, BQ=AQ=AC
, и двум прилежащим к ней углам:
\angle BQC=\angle AQC-\angle AQB=70^{\circ}-60^{\circ}=10^{\circ}=\angle ACP,
\angle CBQ=\angle ABC-\angle ABQ=80^{\circ}-60^{\circ}=20^{\circ}=\angle PAC.
Следовательно, AP=BC
. Что и требовалось доказать.
Примечание. Из единственности следует и обратное: если точка P
лежит на стороне AB
треугольника ABC
с углом \angle ABC=80^{\circ}
, и при этом \angle BPC=30^{\circ}
и AP=BC
, то треугольник ABC
равнобедренный с углом 20^{\circ}
при вершине A
.
Источник: Журнал «Crux Mathematicorum». — 2001, № 1, задача 3, с. 1; 2000, № 5, задача 3, с. 257
Источник: Канадские математические олимпиады. — 2000
