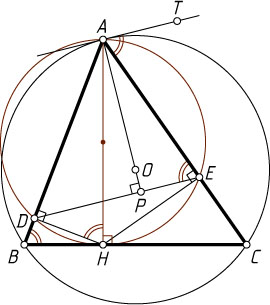
13664. На высоте AH
треугольника ABC
как на диаметре построена окружность, пересекающая AB
и AC
в точках соответственно D
и E
, отличных от A
. Докажите, что центр описанной окружности треугольника ABC
лежит на прямой, содержащей высоту треугольника ADE
, проведённую из вершины A
.
Решение. Рассмотрим случай, изображённый на рисунке. Для остальных случаев решение аналогично.
Точка D
лежит на окружности с диаметром AH
, поэтому \angle ADH=90^{\circ}
. Тогда
\angle AED=\angle AHD=\angle ABH=\angle ABC.
На касательной к описанной окружности треугольника ABC
отметим точку T
, лежащую с точкой B
по разные стороны от прямой AC
. Тогда из теоремы об угле между касательной и хордой следует, что
\angle EAT=\angle CAT=\angle ABC=\angle AED.
Значит, AT\parallel DE
.
Пусть O
— центр описанной окружности треугольника ABC
. Тогда OA\perp AT
, следовательно, OA\perp DE
, т. е. точка O
лежит на прямой, содержащей высоту AP
треугольника ADE
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2001, № 1, задача 3, с. 17