1370. Из вершины A
треугольника ABC
опущены перпендикуляры AM
и AP
на биссектрисы внешних углов B
и C
. Докажите, что отрезок PM
равен половине периметра треугольника ABC
.
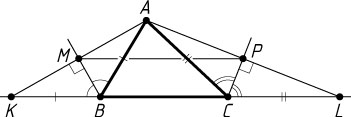
Указание. Пусть прямые AM
и AP
пересекают прямую BC
в точках K
и L
. Тогда отрезок KL
равен половине периметра исходного треугольника, а MP
— средняя линия треугольника AKL
.
Решение. Пусть прямые AM
и AP
пересекают прямую BC
в точках K
и L
. Поскольку высоты BM
и CP
треугольников ABK
и ACL
являются их биссектрисами, то эти треугольники равнобедренные, поэтому BK=AB
и CL=AC
. Значит, отрезок KL
равен периметру треугольника ABC
.
Высоты BM
и CP
равнобедренных треугольников ABK
и ACL
являются их медианами, поэтому точки M
и P
— середины отрезков AK
и AL
. Значит, MP
— средняя линия треугольника AKL
. Следовательно, отрезок MP
равен половине отрезка KL
, т. е. половине периметра треугольника ABC
.
Источник: Зубелевич Г. И. Сборник задач московских математических олимпиад. — 2-е изд. — М.: Просвещение, 1971. — № 615
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 401, с. 48
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.18, с. 24
