1371. На боковых сторонах AB
и BC
равнобедренного треугольника ABC
взяты соответственно точки M
и N
так, что BM=CN
. Докажите, что середина отрезка MN
лежит на средней линии треугольника ABC
, параллельной его основанию.
Указание. Продолжите среднюю линию треугольника до пересечения с прямой, проходящей через точку N
параллельно AB
.
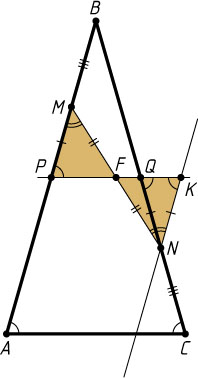
Решение. Пусть P
и Q
— середины сторон AB
и BC
. Предположим, что BM\lt BP
. Тогда
PM=BP-BM=CQ-CN=QN.
Через точку N
проведём прямую, параллельную AB
. Пусть K
— точка пересечения этой прямой с прямой PQ
, а F
— точка пересечения прямых PQ
и MN
. Тогда KN=QN=PM
. Значит, треугольники FKN
и FPM
равны по стороне и двум прилежащим к ней углам. Следовательно, NF=MF
, т. е. середина F
отрезка MN
принадлежит средней линии PQ
треугольника ABC
.
Аналогично для случая, когда BM\gt BP
.
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 6, с. 4
