1372. В равнобедренном треугольнике высота, проведённая к основанию, делится точкой пересечения высот пополам. Найдите углы этого треугольника.
Ответ. 2\arctg\frac{1}{\sqrt{2}}
, 90^{\circ}-\arctg\frac{1}{\sqrt{2}}
, 90^{\circ}-\arctg\frac{1}{\sqrt{2}}
.
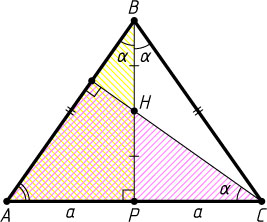
Решение. Пусть BP
— высота равнобедренного треугольника ABC
, проведённая к основанию AC
, H
— точка пересечения высот треугольника. Обозначим
\angle ABP=\angle CBP=\alpha,~AC=2a.
Тогда
\angle HCP=\alpha,~BP=\frac{AP}{\tg\angle ABP}=\frac{a}{\tg\alpha},~HP=CP\tg\angle HCP=a\tg\alpha.
По условию BP=2HP
, или
\frac{a}{\tg\alpha}=2a\tg\alpha,
откуда \tg\alpha=\frac{1}{\sqrt{2}}
.
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 9, с. 5
