13721. Разрежьте треугольник на пять вписанных четырёхугольников.
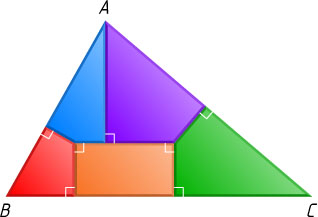
Решение. Первый способ. См. рис. 1 (A
— наибольший угол треугольника).
Второй способ. Отметим внутри треугольника XYZ
точку T
, проекции X'
, Y'
и Z'
которой на стороны треугольника лежат внутри сторон (например, T
— центр вписанной окружности треугольника XYZ
). Тогда отрезки TX'
, TY'
и TZ'
разбивают треугольник на три вписанных четырёхугольника.
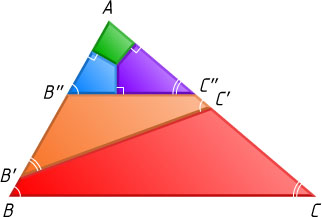
Вернёмся к треугольнику ABC
(рис. 2). Пусть A
— его наибольший угол. Отметим на его сторонах AB
и AC
соответственно точки B'
и C'
, для которых \angle AC'B'=\angle ABC
. Тогда \angle AB'C'=\angle ACB
, и четырёхугольник AB'C'C
вписанный.
На отрезках AC'
и AB'
отметим точки соответственно C''
и B''
, для которых B''C''\parallel BC
. Тогда отрезок B'C'
разбивает трапецию BCC''B''
на два вписанных четырёхугольника. Разбив при этом треугольник AB''C''
на три вписанных четырёхугольника, получим ещё одно разбиение треугольника ABC
на пять вписанных четырёхугольников.
Примечание. Чтобы получить разбиение треугольника ABC
на четыре вписанных четырёхугольника, можно отрезать от него вписанный четырёхугольник, а оставшийся треугольник разрезать на три вписанных четырёхугольника указанным выше способом.
Методом математической индукции можно доказать, что любой треугольник можно разрезать на n
вписанных четырёхугольников для любого n\geqslant3
.
Источник: Журнал «Crux Mathematicorum». — 2003, № 5, задача 2754 (2002, с. 330), с. 333

