13775. В треугольнике ABC
(AB\ne AC
) проведена высота AD
. Биссектрисы BE
и CF
треугольника пересекают AD
в точках B'
и C'
, а сами пересекаются в точке A'
. На стороне BC
отмечены точки P
и Q
, причём BP=AB
и CQ=AC
. Докажите, что треугольники A'B'C'
и AQP
подобны.
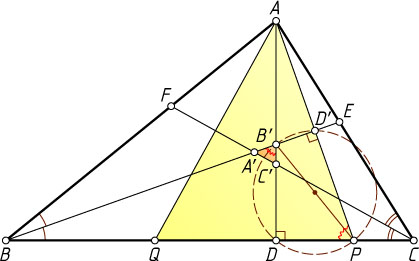
Решение. Рассмотрим случай, изображённый на рисунке.
Пусть D'
— точка пересечения AP
и BE
. Треугольник ABP
равнобедренный, поэтому его биссектриса BE
является высотой.
Из точек D
и D'
отрезок PB'
виден под прямым углом, значит, эти точки лежат на окружности с диаметром B'P
, и PDB'D'
— вписанный четырёхугольник. Тогда
\angle A'B'C'=\angle A'B'D=180^{\circ}-\angle DB'D'=\angle DPD'=\angle APQ.
Аналогично, \angle A'C'B'=\angle AQP
. Следовательно, треугольники A'B'C'
и AQP
подобны по двум углам. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2006, № 1, задача 3003 (2005, с. 43, 46), с. 55
