13781. В прямоугольном треугольнике ABC
с прямым углом при вершине C
проведена высота CF
. Окружность с центром B
, проходящая через точку F
, и окружность того же радиуса с центром A
пересекаются на стороне BC
. Найдите отношение \frac{FB}{BC}
.
Ответ. \frac{1}{\sqrt[{3}]{{2}}}
.
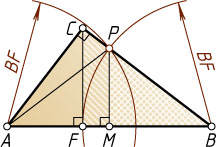
Решение. Пусть окружность с центром B
, проходящая через точку F
, пересекает катет BC
в точке P
, а M
— основание перпендикуляра, опущенного из точки P
на прямую BC
. Тогда
AP=BF=BP,
поэтому PM
— высота равнобедренного треугольника APB
. Значит, M
— середина гипотенузы AB
.
Из подобия треугольников PBM
и CBF
получаем, что \frac{BP}{MB}=\frac{BC}{FB}
; из подобия треугольников ABC
и CBF
получаем, что \frac{AB}{BC}=\frac{BC}{BF}
. Значит,
\frac{FB}{BC}=\frac{FB}{MB}\cdot\frac{MB}{BC}=\frac{BP}{MB}\cdot\frac{\frac{1}{2}AB}{BC}=\frac{1}{2}\frac{BP}{MB}\cdot\frac{AB}{BC}=\frac{1}{2}\cdot\frac{BC}{FB}\cdot\frac{BC}{FB}=\frac{1}{2}\left(\frac{BC}{FB}\right)^{2},
откуда \left(\frac{FB}{BC}\right)^{3}=\frac{1}{2}
. Следовательно, \frac{FB}{BC}=\frac{1}{\sqrt[{3}]{{2}}}
.
Источник: Журнал «Crux Mathematicorum». — 2006, № 3, задача 1, с. 161
Источник: Финские математические олимпиады. — 2002-2002
