13785. Окружность проходит через вершину C
прямоугольника ABCD
и касается сторон AB
и AD
в точках M
и N
соответственно. Расстояние от точки C
до прямой MN
равно 2. Найдите площадь прямоугольника.
Ответ. 4.
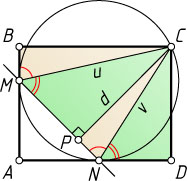
Решение. Пусть P
— основание перпендикуляра, опущенного из вершины C
на прямую MN
. Обозначим CP=d
, CM=u
и CN=v
.
Из теоремы об угле между касательной и хордой следует, что
\angle BMC=\angle MNC=\angle PNC,
поэтому треугольник BMC
подобен треугольнику PNC
. Аналогично, треугольник DNC
подобен треугольнику PMC
. Тогда
\frac{BC}{d}=\frac{u}{v},~\frac{DC}{d}=\frac{v}{u}.
Следовательно,
S_{ABCD}=BC\cdot DC=\frac{du}{v}\cdot\frac{dv}{u}=d^{2}=4.
Источник: Журнал «Crux Mathematicorum». — 2006, № 6, задача 7, с. 381
Источник: Сингапурские математические олимпиады. — 2002
