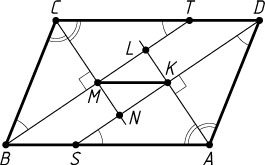
1383. Докажите, что биссектрисы внутренних углов параллелограмма, не являющегося ромбом, при пересечении образуют прямоугольник, диагональ которого равна разности двух соседних сторон параллелограмма.
Решение. Пусть биссектрисы углов при вершинах B
и C
параллелограмма ABCD
пересекаются в точке M
, биссектрисы углов при вершинах C
и D
— в точке N
, углов при вершинах A
и D
— в точке K
, углов при вершинах A
и B
— в точке L
.
Поскольку биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны, то MLKN
— прямоугольник.
Предположим, что AB\gt BC
.
Если луч BM
пересекает прямую CD
в точке T
, то
\angle BTC=\angle TBA=\angle CBT.
Значит, треугольник BCT
— равнобедренный. Поэтому
CT=BC\lt AB=CD.
Следовательно, точка T
лежит между точками C
и D
и
DT=CD-CT=AB-BC.
Поскольку CM
— высота равнобедренного треугольника, проведённая к основанию, то M
— середина BT
. Аналогично докажем, что если S
— точка пересечения луча DK
со стороной AB
, то K
— середина DS
. Точки M
и K
— середины противоположных сторон параллелограмма BTDS
. Следовательно,
MK=DT=AB-BC
Поскольку диагонали прямоугольника равны, то LN=MK=AB-BC
.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 8, с. 196
Источник: Вступительный экзамен в МФТИ. — 1949, билет 11, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 49-11-3, с. 18
Источник: Зубелевич Г. И. Сборник задач московских математических олимпиад. — 2-е изд. — М.: Просвещение, 1971. — № 618, с. 68
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.9, с. 23
