1385. Диагонали ромба ABCD
пересекаются в точке O
. Докажите, что точки пересечения биссектрис каждого из треугольников ABO
, BCO
, CDO
и DAO
являются вершинами квадрата.
Указание. Докажите, что диагонали указанного четырёхугольника взаимно перпендикулярны и делятся точкой их пересечения пополам, а стороны параллельны диагоналям данного ромба.
Решение. Пусть M
, N
, K
и L
— точки пересечения биссектрис треугольников ABO
, BCO
, CDO
и DAO
соответственно. Тогда прямые MK
и NL
проходят через точку O
и MK\perp NL
.
Треугольники BOM
и DOK
равны по стороне (OB=OD
) и двум прилежащим к ней углам, поэтому MO=OK
. Аналогично NO=OL
. Значит, MNKL
— параллелограмм, диагонали которого взаимно перпендикулярны, т. е. ромб.
Пусть BP
и BQ
— биссектрисы равных треугольников ABO
и CBO
. Тогда по свойству биссектрисы треугольника
\frac{BM}{MP}=\frac{BO}{OP}=\frac{BO}{OQ}=\frac{BN}{NQ},
поэтому MN\parallel AC
. Аналогично ML\parallel BD
. Поскольку AC\perp BD
, то \angle LMN=90^{\circ}
. Следовательно, MNKL
— квадрат.
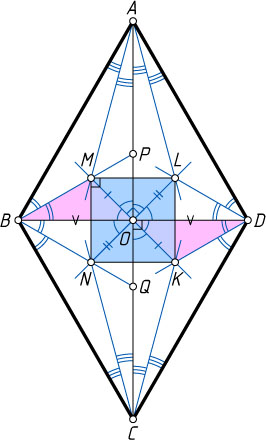
Источник: Зубелевич Г. И. Сборник задач московских математических олимпиад. — 2-е изд. — М.: Просвещение, 1971. — № 620, с. 68
