13900. Окружности \Gamma_{1}
и \Gamma_{2}
радиуса r
с центрами A
и B
соответственно пересекаются в точках C
и D
, причём \angle BCA=90^{\circ}
. Прямая, проходящая через точку C
пересекает окружности \Gamma_{1}
и \Gamma_{2}
в точках E
и F
, причём точка C
лежит между E
и F
. Окружность \Gamma
с центром O
и радиусом R
проходит через точки E
и F
. Вторая прямая проходит через точку C
перпендикулярно EF
и пересекает окружность \Gamma
в точках G
и H
. Докажите, что CH^{2}+CG^{2}=4(R^{2}-r^{2})
.
Решение. Рассмотрим случай, изображённый на чертеже.
Пусть M
и N
— середины EC
и CF
соответственно, и AM=a
и BN=b
. Поскольку
\angle ACM=90^{\circ}-\angle BCN=\angle CBN,
поэтому прямоугольные треугольники AMC
и CNB
равны по гипотенузе и острому углу. Тогда
AM=CN=a,~BN=MC=b,
EF=2MN=2(MC+CN)=2(b+a).
Пусть P
— середина отрезка EF
. Тогда
EP=\frac{1}{2}EF=b+a,~MP=EP-EM=(b+a)-b=a,
PC=EP-EC=(a+b)-2b=a-b.
Пусть Q
— середина отрезка GH
, PO=CQ=h
. Тогда
OQ=PC=a-b~\Rightarrow~QH^{2}=OH^{2}-OQ^{2}=R^{2}-(b-a)^{2}.
Значит,
CH^{2}+CG^{2}=(CQ+QH)^{2}+(GQ-CQ)^{2}=
=(h+QH)^{2}+(QH-h)^{2}=2(QH^{2}+h^{2}),
а так как
R^{2}=OF^{2}=CQ^{2}+FP^{2}=h^{2}+(b+a)^{2},
то
h^{2}=R^{2}-(b+a)^{2}.
Следовательно,
CH^{2}+CG^{2}=2(R^{2}-(b-a)^{2}+R^{2}-(b+a)^{2})=
=2(2R^{2}-2(b^{2}+a^{2}))=2(2R^{2}-2r^{2})=4(R^{2}-r^{2}).
Что и требовалось доказать.
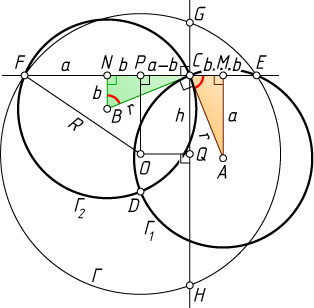
Источник: Журнал «Crux Mathematicorum». — 2011, № 7, задача 3582 (2010, с. 460, 462), с. 468
