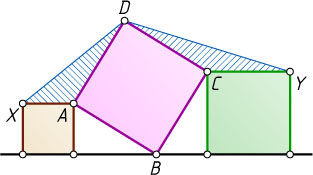
13901. Три квадрата расположены так, как показано на рисунке. Докажите, что треугольники ADX
и CDY
равновелики.
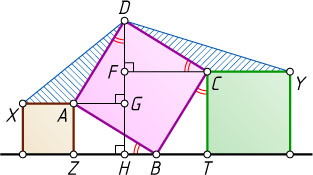
Решение. Обозначим AX=a
, CY=b
. Опустим перпендикуляры: DH
на прямую ZT
, AG
на прямую DH
, CF
на прямую DH
. Из параллельности AB
и CD
следует равенство углов ABZ
и DCF
прямоугольных треугольников AZB
и DFC
, поэтому эти треугольники равны по гипотенузе и острому углу. Значит, DF=AZ=a
. Аналогично, DG=CT=b
. Следовательно,
S_{\triangle ADX}=\frac{1}{2}AX\cdot DG=\frac{1}{2}ab=\frac{1}{2}DF\cdot CY=S_{\triangle CDY}.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2011, № 8, задача 4, с. 485

