1391. В квадрате ABCD
из точки D
как из центра проведена внутри квадрата дуга через вершины A
и C
. На AD
как на диаметре построена внутри квадрата полуокружность. Отрезок прямой, соединяющей произвольную точку P
дуги AC
с точкой D
, пересекает полуокружность AD
в точке K
. Докажите, что длина отрезка PK
равна расстоянию от точки P
до стороны AB
.
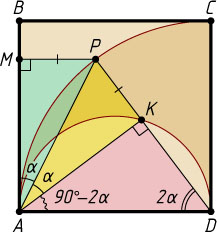
Решение. Пусть M
— проекция точки P
на AB
. Обозначим \angle MAP=\alpha
. Поскольку MAP
— угол между касательной AB
и хордой AP
первой окружности, то
\angle ADK=\angle ADP=2\alpha.
Из прямоугольного треугольника AKD
находим, что
\angle KAD=90^{\circ}-\angle ADK=90^{\circ}-2\alpha,
поэтому
\angle KAP=90^{\circ}-\angle MAP-\angle KAD=90^{\circ}-\alpha-(90^{\circ}-2\alpha)=\alpha.
Значит, прямоугольные треугольники KAP
и MAP
равны по гипотенузе и острому углу. Следовательно, PK=PM
.
Источник: Зубелевич Г. И. Сборник задач московских математических олимпиад. — 2-е изд. — М.: Просвещение, 1971. — № 634, с. 70
