13913. Окружности \Gamma_{1}
и \Gamma_{2}
пересекаются в точках A
и B
. Точки P
и R
лежат на этих окружностях, как показано на рисунке. С помощью одной линейки постройте середину отрезка PR
.
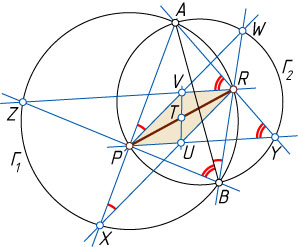
Решение. Пусть прямая AP
вторично пересекает окружность \Gamma_{1}
в точке X
, прямая прямая AR
вторично пересекает окружность \Gamma_{2}
в точке Y
, прямая BP
вторично пересекает окружность \Gamma_{1}
в точке Z
, прямая BR
окружность \Gamma_{2}
в точке W
, прямые XR
и YP
пересекаются в точке U
, прямые ZR
и WP
— в точке V
, а прямые UV
и PR
— в точке T
. Тогда точка T
— искомая середина отрезка PR
.
Действительно, поскольку
\angle VPA=\angle WPA=\angle WBA=\angle RBA=\angle RXA,
прямые VP
и RU
параллельны. Поскольку
\angle ZRA=\angle ZBA=\angle PBA=\angle PYA,
прямые VR
и PU
параллельны. Значит, PURV
— параллелограмм. Точка T
пересечения его диагоналей — середина отрезка PR
.
Источник: Журнал «Crux Mathematicorum». — 2022, № 6, задача 4706, с. 361

