13970. Точка P
лежит на вписанной окружности \Gamma
треугольника ABC
. Прямые, проведённые через точку P
перпендикулярно сторонам BC
, CA
и AB
, вторично пересекают окружность \Gamma
в точках U
, V
и W
соответственно. Докажите, что одно из произведений PU\cdot BC
, PV\cdot CA
и PW\cdot AB
равно сумме двух других.
Решение. Обозначим углы треугольника ABC
при вершинах A
, B
и C
через \alpha
, \beta
и \gamma
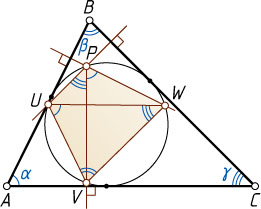
соответственно. Рассмотрим случай, изображённый на рисунке.
Поскольку PV\perp CA
и PW\perp AB
, то \sin\angle VPW=\sin\angle BAC=\sin\alpha
. Аналогично,
\sin\angle WPU=\sin\beta,~\sin\angle UPV=\sin\gamma,
а так как четырёхугольник PUVW
вписанный, то
\sin\angle VPW=\sin\angle VUW,~\sin\angle WPU=\sin\angle WVU,~\sin\angle UPV=\sin\angle UWV.
По теореме синусов
\frac{WV}{WU}=\frac{\sin\angle VUW}{\sin\angle WVU}~\mbox{и}~\frac{UV}{WU}=\frac{\sin\angle UWV}{\sin\angle WVU},
а также
\frac{\sin\alpha}{\sin\beta}=\frac{BC}{CA}~\mbox{и}~\frac{\sin\gamma}{\sin\beta}=\frac{AB}{CA}.
Тогда по теореме Птолемея для вписанного четырёхугольника получаем,
PV\cdot WU=PU\cdot VW+PW\cdot UV.
Значит,
PV=PU\cdot\frac{VW}{WU}+PW\cdot\frac{UV}{WU}=PU\cdot\frac{\sin\angle VUW}{\sin\angle WVU}+PW\cdot\frac{\sin\angle UWV}{\sin\angle WVU}=
=PU\cdot\frac{\sin\angle VPW}{\sin\angle WPU}+PW\cdot\frac{\sin\angle UPV}{\sin\angle WPU}=
=PU\cdot\frac{\sin\alpha}{\sin\beta}+PW\cdot\frac{\sin\gamma}{\sin\beta}=PU\cdot\frac{BC}{CA}+PW\cdot\frac{AB}{CA}.
Следовательно,
PV\cdot CA=PU\cdot BC+PW\cdot AB.
Что и требовалось доказать.
Аналогично для остальных случаев.
Источник: Журнал «Crux Mathematicorum». — 2016, № 2, задача 4017, с. 86
