13981. Точки D
и E
расположены внутри равностороннего треугольника ABC
, причём DA=DB=EA=EC
и DE=2
(см. рис.). Найдите сторону треугольника ABC
.
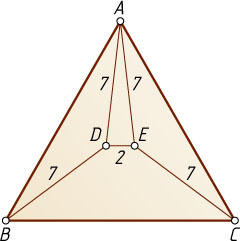
Ответ. 13.
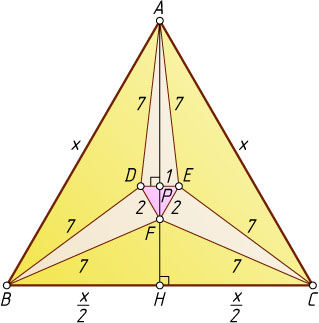
Решение. Пусть F
— вершина равнобедренного треугольника с основанием BC
и боковыми сторонами BF=CE=7
. Тогда треугольник BFC
равен треугольникам ADB
и AEC
по трём сторонам. Значит, треугольники BDF
и CEF
равны треугольнику ADE
по двум сторонам и углу между ними. Тогда DF=EF=DE=2
, поэтому треугольник DEF
равносторонний.
Обозначим AB=BC=CA=x
. Пусть AH
— высота треугольника ABC
. Сумма высот AP
равнобедренного треугольника ADE
, FP
равностороннего треугольника DEF
и FH
равнобедренного треугольника BFC
равна AH
, т. е.
\sqrt{49-1}+2\cdot\frac{\sqrt{3}}{2}+\sqrt{49-\frac{x^{2}}{4}}=\frac{x\sqrt{3}}{2}~\Leftrightarrow
\Leftrightarrow~\sqrt{4\cdot49-x^{2}}=\sqrt{3}(x-10)~\Rightarrow~x^{2}-15x+26=0.
Условию задачи удовлетворяет x=13
.
Источник: Журнал «Crux Mathematicorum». — 2017, № 5, задача CC222, с. 191

