13997. Вершина E
равностороннего треугольника ABE
лежит внутри квадрата ABCD
со стороной 4. Отрезки AC
и BE
пересекаются в точке P
. Найдите площадь треугольника APE
.
Ответ. 8\sqrt{3}-12
.
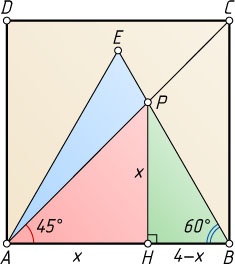
Решение. Опустим перпендикуляр PH
на сторону AB
квадрата. Поскольку \angle PAH=45^{\circ}
, треугольник AHP
прямоугольный и равнобедренный. Обозначим AH=HP=x
. Тогда BH=4-x
. Из прямоугольного треугольника BHP
получаем
x=HP=BH\tg60^{\circ}=(4-x)\sqrt{3},
откуда
x=\frac{4\sqrt{3}}{\sqrt{3}+1}=6-2\sqrt{3}.
Следовательно,
S_{\triangle APE}=S_{\triangle ABE}-S_{\triangle ABP}=\frac{AB^{2}\sqrt{3}}{4}-\frac{1}{2}AB\cdot PH=
=4\sqrt{3}-2x=4\sqrt{3}-2(6-2\sqrt{3})=8\sqrt{3}-12.
Источник: Журнал «Crux Mathematicorum». — 2019, № 2, задача CC319, с. 63
