1407. Окружности с центрами O_{1}
и O_{2}
пересекаются в точках A
и B
. Известно, что \angle AO_{1}B=90^{\circ}
, \angle AO_{2}B=60^{\circ}
, O_{1}O_{2}=a
. Найдите радиусы окружностей.
Ответ. \frac{a\sqrt{2}}{\sqrt{3}+1}
, \frac{2a}{\sqrt{3}+1}
или \frac{a\sqrt{2}}{\sqrt{3}-1}
, \frac{2a}{\sqrt{3}-1}
.
Указание. Рассмотрите два случая: центры окружностей лежат по разные стороны от общей хорды; центры окружностей лежат по одну сторону от общей хорды.
Решение. Пусть линия центров O_{1}O_{2}
пересекает общую хорду AB
окружностей в точке M
. Тогда M
— середина AB
и O_{1}O_{2}\perp AB
. Треугольник AO_{1}B
— прямоугольный и равнобедренный, а треугольник AO_{2}B
— равносторонний, поэтому, если r
и R
— радиусы окружностей с центрами O_{1}
и O_{2}
соответственно, то AB=r\sqrt{2}
и AB=R
, значит, R=r\sqrt{2}
. Тогда
O_{1}M=\frac{r\sqrt{2}}{2},~O_{2}M=\frac{R\sqrt{3}}{2}=\frac{r\sqrt{2}\cdot\sqrt{3}}{2}=\frac{r\sqrt{6}}{2}
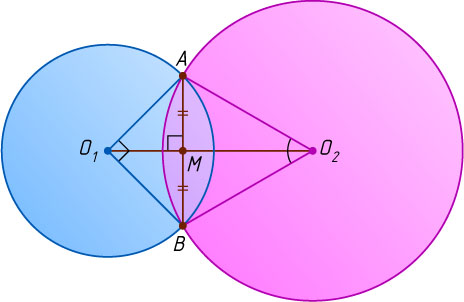
Предположим, что центры окружностей лежат по разные стороны от прямой AB
. Тогда O_{1}M+MO_{2}=O_{1}O_{2}
, или \frac{r\sqrt{2}}{2}+\frac{r\sqrt{6}}{2}=a
. Отсюда находим, что
r=\frac{a\sqrt{2}}{\sqrt{3}+1},~R=r\sqrt{2}=\frac{2a}{\sqrt{3}+1}.
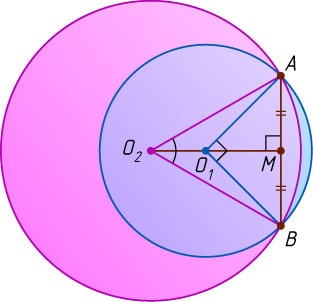
Если же точки O_{1}
и O_{2}
лежат по одну сторону от прямой AB
, то O_{2}M-MO_{1}=O_{1}O_{2}
. Тогда
r=\frac{a\sqrt{2}}{\sqrt{3}-1},~R=r\sqrt{2}=\frac{2a}{\sqrt{3}-1}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 84, с. 13
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 84, с. 12
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.2, с. 76

