14156. В прямоугольном параллелепипеде ABCDA_{1}B_{1}C_{1}D_{1}
известны рёбра AB=5
, AD=12
, AA_{1}=8
.
а) Докажите, что плоскость DB_{1}B
образует равные углы с плоскостями CD_{1}B_{1}
и AD_{1}B_{1}
.
б) Найдите угол между плоскостями CD_{1}B_{1}
и AD_{1}B_{1}
.
Ответ. 2\arctg\frac{15}{26}
.
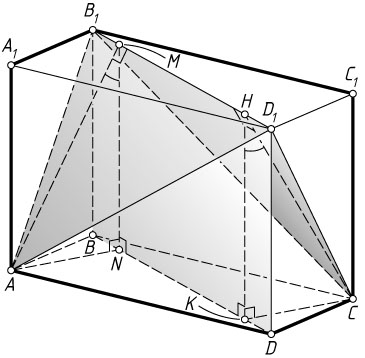
Решение. а) В треугольниках CD_{1}B_{1}
и AD_{1}B_{1}
проведём высоты CH
и AM
. Из точек H
и M
опустим перпендикуляры HK
и MN
на прямую BD
. Тогда HK
и MN
перпендикуляры к плоскости оснований параллелепипеда. Поскольку наклонные CH
и AM
перпендикулярны прямой DB
, то по теореме о трёх перпендикулярах их проекции KC
и AN
перпендикулярны прямой DB
, а так как ABCD
— прямоугольник, то CK=AN
как соответствующие высоты равных треугольников BCD
и DAB
. Тогда прямоугольные треугольники CKH
и ANM
равны по двум катетам, поэтому \angle KHC=\angle NMA
, т. е. плоскость DBB_{1}
образует равные углы с плоскостями CD_{1}B_{1}
и AD_{1}B_{1}
.
б) Угол между плоскостями CD_{1}B_{1}
и AD_{1}B_{1}
равен сумме углов, которые плоскость DBB_{1}
образует с плоскостями CD_{1}B_{1}
и AD_{1}B_{1}
.
Из треугольников DCB
и KHC
находим, что
BD=13,~CK=\frac{DC\cdot CB}{DB}=\frac{12\cdot5}{13}=\frac{60}{13},
\tg\angle KHC=\frac{CK}{KH}=\frac{\frac{60}{13}}{8}=\frac{15}{26}.
Аналогично, \tg\angle NMA=\frac{15}{26}
. Следовательно, угол между плоскостями CD_{1}B_{1}
и AD_{1}B_{1}
равен 2\arctg\frac{15}{26}
.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2021
