14171. Дана прямая треугольная призма ABCA_{1}B_{1}C_{1}
. Известно, что AB=BC
. Точка K
— середина ребра A_{1}B_{1}
, а точка M
лежит на ребре AC
и делит его в отношении AM:MC=1:3
.
а) Докажите, что прямая KM
перпендикулярна прямой AC
.
б) Найдите расстояние между прямыми KM
и A_{1}C_{1}
, если AB=6
, AC=8
и AA_{1}=3
.
Ответ. \frac{3\sqrt{70}}{14}
.
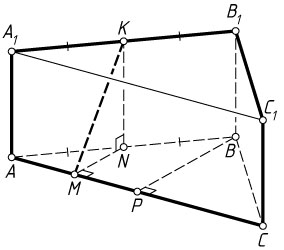
Решение. а) Пусть BP
— высота и медиана равнобедренного треугольника ABC
, N
— середина ребра AB
. Тогда M
— середина отрезка AP
, а NM
— средняя линия прямоугольного треугольника ABM
. Значит, NM\parallel BP
, поэтому NM\perp AC
.
Отрезок NM
— ортогональная проекция наклонной KM
на плоскость ABC
. Следовательно, по теореме о трёх перпендикулярах KM\perp AC
.
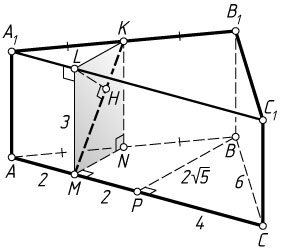
б) Пусть L
— точка на ребре A_{1}C_{1}
, для которой A_{1}L:LC_{1}=AM:MC=1:3
. Тогда прямая A_{1}C_{1}
перпендикулярна плоскости MKL
. Пусть LH
— высота прямоугольного треугольника MKL
. Тогда LH\perp KM
и LH\perp A_{1}C_{1}
, значит, LH
— общий перпендикуляр скрещивающихся прямых KM
и A_{1}C_{1}
, а искомое расстояние между этими прямыми равно длине LH
. Из прямоугольного треугольника MKL
с катетами
LM=AA_{1}=3,~KL=NM=\frac{1}{2}BP=\frac{1}{2}\sqrt{AB^{2}-AP^{2}}=\frac{1}{2}\sqrt{36-16}=\sqrt{5}
и гипотенузой
KM=\sqrt{LM^{2}+KL^{2}}=\sqrt{9+5}=\sqrt{14}
находим, что
LH=\frac{KL\cdot LM}{KM}=\frac{\sqrt{5}\cdot3}{\sqrt{14}}=\frac{3\sqrt{5}}{\sqrt{14}}=\frac{3\sqrt{70}}{14}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2020

