1421. На одной из сторон угла, равного \alpha
(\alpha\lt90^{\circ}
), с вершиной в точке O
взяты точки A
и B
, причём OA=a
, OB=b
. Найдите радиус окружности, проходящей через точки A
и B
и касающейся другой стороны угла.
Ответ. \frac{a+b-2\sqrt{ab}\cos\alpha}{2\sin\alpha}
.
Указание. Пусть D
— точка касания окружности с другой стороной угла. Найдите коэффициент подобия треугольников ODB
и OAD
. Искомый радиус найдите по обобщённой теореме синусов из треугольника ABD
.
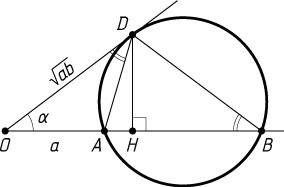
Решение. Пусть D
— точка касания окружности с другой стороной угла, H
— проекция точки D
на прямую AB
, R
— искомый радиус. По теореме о касательной и секущей находим, что OD=\sqrt{ab}
. Тогда по теореме косинусов
AD^{2}=ab+a^{2}-2a\sqrt{ab}\cos\alpha=a(a+b-2\sqrt{ab}\cos\alpha).
Треугольники ODB
и OAD
подобны (по двум углам) с коэффициентом
k=\frac{OB}{OD}=\frac{b}{\sqrt{ab}}=\frac{\sqrt{b}}{\sqrt{a}}.
Из прямоугольного треугольника DHB
находим, что
\sin\angle DBH=\frac{DH}{DB}=\frac{OD\cdot\sin\alpha}{DB}=\frac{\sqrt{ab}\sin\alpha}{kAD}.
Значит,
R=\frac{AD}{2\sin\angle DBH}=\frac{kAD^{2}}{2\sqrt{ab}\sin\alpha}=\frac{\frac{\sqrt{b}}{\sqrt{a}}\cdot a(a+b-2\sqrt{ab}\cos\alpha)}{2\sqrt{ab}\sin\alpha}=\frac{a+b-2\sqrt{ab}\cos\alpha}{2\sin\alpha}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1965, вариант 8, № 4
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 8, № 4, с. 293
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 51, с. 163
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.27, с. 95
