1426. Центры трёх окружностей, попарно касающихся друг друга внешним образом, расположены в вершинах прямоугольного треугольника. Эти окружности касаются изнутри четвёртой окружности. Найдите радиус четвёртой окружности, если периметр прямоугольного треугольника равен 2p
.
Ответ. p
.
Указание. Достройте данный прямоугольный треугольник до прямоугольника. Докажите, что центр четвёртой окружности расположен в достроенной вершине прямоугольника.
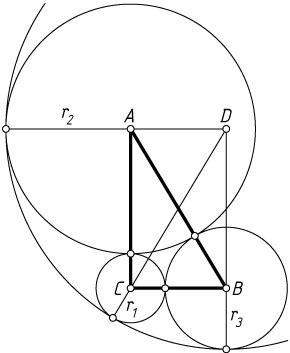
Решение. Рассмотрим прямоугольный треугольник ABC
(\angle C=90^{\circ}
), в вершинах которого расположены центры окружностей. Обозначим радиусы этих окружностей через r_{1}
, r_{2}
, r_{3}
, причём
AC=r_{1}+r_{2},~BC=r_{1}+r_{3},~AB=r_{2}+r_{3}.
Построим окружность радиуса p
с центром в вершине D
прямоугольника ACBD
. Поскольку
DC=AB=r_{2}+r_{3}=p-r_{1},~DA=p-r_{2},~DB=p-r_{3},
то окружности с центрами в точках C
, A
и B
касаются изнутри окружности с центром в точке D
. Осталось доказать, что найденная окружность единственная.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.6.11, с. 156
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 703, с. 89
