1430. Найдите углы треугольника, если известно, что медиана и высота, выходящие из вершины одного из его углов, делят этот угол на три равные части.
Ответ. 30^{\circ}
, 60^{\circ}
, 90^{\circ}
.
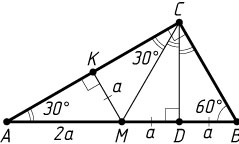
Решение. Пусть высота CD
и медиана CM
делят угол C
треугольника ABC
на три равные части. Предположим, что точка D
расположена между B
и M
. Обозначим \angle BCD=\angle DCM=\angle ACM=\alpha
. Поскольку в треугольнике BCM
высота CD
является биссектрисой, то этот треугольник равнобедренный, поэтому CD
— медиана треугольника BCM
и BD=DM
.
Первый способ. Пусть K
— проекция точки M
на AC
. Тогда из равенства прямоугольных треугольников CKM
и CDM
(по гипотенузе и острому углу) следует, что
MK=DM=\frac{1}{2}BM=\frac{1}{2}AM.
Значит, \angle MAK=30^{\circ}
. Следовательно,
2\alpha=\angle ACD=90^{\circ}-\angle MAK=90^{\circ}-30^{\circ}=60^{\circ},~\alpha=30^{\circ},
\angle ACB=3\alpha=90^{\circ},~\angle ABC=60^{\circ}.
Второй способ. Биссектриса CM
треугольника ACD
делит сторону AD
на отрезки, пропорциональные сторонам AC
и CD
, т. е.
\frac{CD}{AC}=\frac{DM}{AM}=\frac{DM}{BM}=\frac{1}{2}.
Значит, \angle CAD=30^{\circ}
. Следовательно,
2\alpha=\angle ACD=90^{\circ}-\angle CAD=90^{\circ}-30^{\circ}=60^{\circ},~\alpha=30^{\circ},
\angle ACB=3\alpha=90^{\circ},~\angle ABC=60^{\circ}.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 151, с. 175
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 47, с. 162
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 19, с. 31
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1.35, с. 14
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1.35.1, с. 14
