1431. Два квадрата ABCD
и KLMN
расположены так, что вершины B
, C
, K
и N
лежат на одной прямой, а четыре оставшиеся расположены по разные стороны от BC
и лежат на одной окружности. Известно, что сторона одного из квадратов на 1 больше стороны другого. Найдите расстояние от центра окружности до прямой BC
.
Ответ. \frac{5}{8}
.
Указание. Обозначьте через x
и x+1
стороны квадратов, через a
— искомое расстояние, опустите перпендикуляры из центра окружности на сторону каждого квадрата, выразите квадрат радиуса окружности из полученных прямоугольных треугольников через x
и a
и, приравняв полученные выражения, решите уравнение относительно a
.
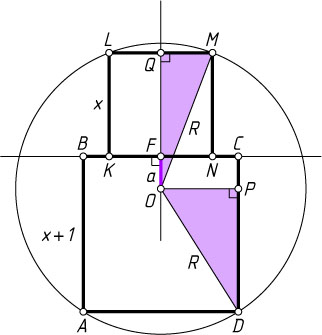
Решение. Обозначим через x
сторону квадрата KLMN
. Пусть сторона квадрата ABCD
равна x+1
; прямая, проходящая через центр O
указанной окружности перпендикулярно прямой BC
, пересекает BC
в точке F
, а LM
— в точке Q
; P
— проекция точки O
на DC
; R
— радиус окружности; OF=a
. Тогда из прямоугольных треугольников OQM
и OPD
находим, что
R^{2}=OM^{2}=OQ^{2}+QM^{2}=(a+x)^{2}+\frac{x^{2}}{4};
R^{2}=OP^{2}+DP^{2}=\frac{(x+1)^{2}}{4}+(x+1-a)^{2}.
Приравняв правые части этих равенств, получим уравнение
(a+x)^{2}+\frac{x^{2}}{4}=\frac{(x+1)^{2}}{4}+(x+1-a)^{2}.
После очевидных упрощений это уравнение примет вид
(2x+1)(8a-5)=0,
откуда находим, что a=\frac{5}{8}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.6.9, с. 156
