1432. Вершина угла величиной 70^{\circ}
служит началом луча, образующего с его сторонами углы 30^{\circ}
и 40^{\circ}
. Из некоторой точки M
на этот луч и на стороны угла опущены перпендикуляры, основания которых — A
, B
и C
. Найдите углы треугольника ABC
.
Ответ. 30^{\circ}
, 40^{\circ}
, 110^{\circ}
.
Указание. Вершина угла и точки M
, A
, B
и C
лежат на одной окружности.
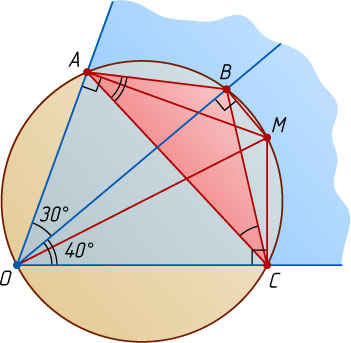
Решение. Пусть A
и C
— основания перпендикуляров, опущенных из точки M
на стороны данного угла с вершиной O
, точка B
— основание перпендикуляра, опущенного из точки M
на луч, проходящий между сторонами угла AOC
, причём \angle AOB=30^{\circ}
и \angle COB=40^{\circ}
.
Из точек A
, B
и C
отрезок OM
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OM
. Вписанные в эту окружность углы ACB
и AOB
опираются на одну и ту же дугу, поэтому \angle ACB=\angle AOB=30^{\circ}
. Аналогично, \angle BAC=\angle COB=40^{\circ}
. Следовательно, \angle ABC=180^{\circ}-30^{\circ}-40^{\circ}=110^{\circ}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 62, с. 164
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.17, с. 104
