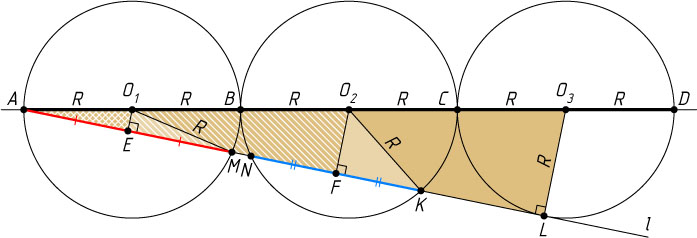
1433. На прямой расположены точки A
, B
, C
и D
, причём AB=BC=CD
. Отрезки AB
, BC
и CD
служат диаметрами окружностей. Из точки A
к окружности с диаметром CD
проведена касательная l
. Найдите отношение хорд, высекаемых на прямой l
окружностями с диаметрами AB
и BC
.
Ответ. \frac{\sqrt{6}}{2}
.
Указание. Опустите перпендикуляры из центров окружностей на прямую l
.
Решение. Пусть O_{1}
, O_{2}
, O_{3}
— центры окружностей с диаметрами AB
, BC
и CD
соответственно; AM
и NK
— хорды, высекаемые на прямой l
первой и второй окружностью; L
— точка касания прямой l
с третьей окружностью; E
и F
— проекции точек O_{1}
и O_{2}
на прямую l
. Обозначим через R
радиусы окружностей.
Треугольник AO_{1}E
подобен треугольнику AO_{3}L
с коэффициентом \frac{1}{5}
, а треугольник AO_{2}F
подобен треугольнику AO_{3}L
с коэффициентом \frac{3}{5}
, поэтому
O_{1}E=\frac{1}{5}O_{3}L=\frac{1}{5}R,~O_{2}F=\frac{3}{5}O_{3}L=\frac{3}{5}R.
Из прямоугольных треугольников O_{1}EM
и O_{2}FK
по теореме Пифагора находим, что
EM=\frac{2R\sqrt{6}}{5},~FK=\frac{4}{5}R.
Следовательно,
\frac{AM}{NK}=\frac{2EM}{2FK}=\frac{EM}{FK}=\frac{\sqrt{6}}{2}.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 58, с. 164
