1435. Отрезки, соединяющие основания высот остроугольного треугольника, равны 8, 15 и 17. Найдите радиус описанной около треугольника окружности.
Ответ. 17.
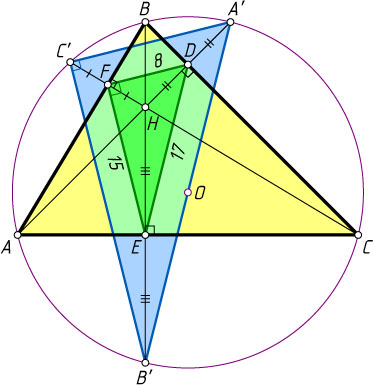
Указание. Продолжите высоты AD
, BE
и CF
данного треугольника ABC
до пересечения с описанной окружностью в точках A'
, B'
и C'
соответственно. Тогда треугольник A'B'C'
подобен треугольнику DEF
с коэффициентом 2.
Решение. Пусть AD
, BE
и CF
— высоты остроугольного треугольника ABC
; H
— точка их пересечения (ортоцентр); DF=8
, EF=15
, DE=17
. Поскольку 8^{2}+15^{2}=17^{2}
, то треугольник DEF
— прямоугольный, \angle DFE=90^{\circ}
.
Продолжим отрезки AD
, BE
и CF
до пересечения с описанной окружностью треугольника ABC
в точках A'
, B'
и C'
соответственно. Поскольку точка, симметричная ортоцентру треугольника, лежит на описанной окружности, то FE
, DE
и DF
— средние линии треугольников B'HC'
, A'HB'
и A'HC'
соответственно. Из этого следует, что треугольник A'B'C'
подобен треугольнику DEF
с коэффициентом 2. Значит, треугольник A'B'C'
— также прямоугольный, его гипотенуза A'B'
равна 34, а радиус описанной окружности равен 17.
