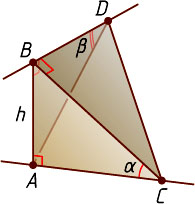
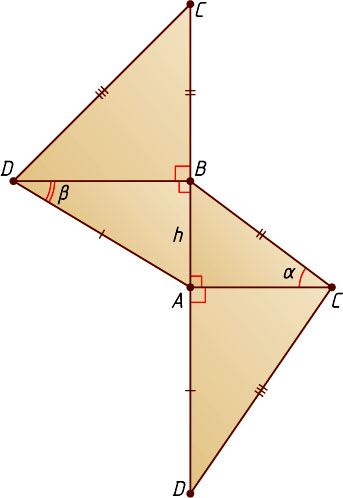
14399. Общий перпендикуляр AB
перпендикулярных скрещивающихся прямых равен h
. На одной из них отмечена точка C
, на другой — точка D
. Отрезок AB
виден из этих точек под углами \alpha
и \beta
соответственно. Найдите полную поверхность пирамиды ABCD
.
Ответ. \frac{h^{2}\cos\frac{\alpha+\beta}{2}\left(\sin\frac{\alpha+\beta}{2}+\cos\frac{\alpha-\beta}{2}\right)}{\sin\alpha\sin\beta}=\frac{2h^{2}\cos\frac{\alpha+\beta}{2}\cos\left(45^{\circ}-\frac{\alpha}{2}\right)\cos\left(45^{\circ}-\frac{\beta}{2}\right)}{\sin\alpha\sin\beta}
.
Решение. Из прямоугольных треугольников ABC
и ABD
находим, что
AC=AB\ctg\angle BCA=h\ctg\alpha,~BC=\frac{AB}{\sin\angle ACB}=\frac{h}{\sin\alpha},
BD=AB\ctg\angle ADB=h\ctg\beta,~AD=\frac{AB}{\sin\angle ADB}=\frac{h}{\sin\beta}.
Значит,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}h^{2}\ctg\alpha,~S_{\triangle ABD}=\frac{1}{2}AB\cdot AD=\frac{1}{2}h^{2}\ctg\beta.
Прямая BD
перпендикулярна пересекающимся прямым AC
и AB
плоскости ABC
, поэтому прямая BD
перпендикулярна плоскости ABC
, а AB
— ортогональная проекция наклонной DA
на эту плоскость. По теореме о трёх перпендикулярах \angle CAD=90^{\circ}
. Следовательно, треугольник CAD
прямоугольный. Значит,
S_{\triangle CAD}=\frac{1}{2}AC\cdot AD=\frac{h^{2}\ctg\alpha}{2\sin\beta}.
Аналогично,
S_{\triangle CBD}=\frac{1}{2}BC\cdot BD=\frac{h^{2}\ctg\beta}{2\sin\alpha}.
Пусть S
— полная поверхность пирамиды ABCD
. Тогда
S=S_{\triangle ABC}+S_{\triangle ABD}+S_{\triangle CAD}+S_{\triangle CBD}=
=\frac{h^{2}}{2}\left(\ctg\alpha+\ctg\beta+\frac{\ctg\alpha}{\sin\beta}+\frac{\ctg\beta}{\sin\alpha}\right)=
=\frac{h^{2}(\cos\alpha\sin\beta+\sin\alpha\cos\beta+\cos\alpha+\cos\beta)}{2\sin\alpha\sin\beta}=
=\frac{h^{2}\left(\sin(\alpha+\beta)+2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\right)}{2\sin\alpha\sin\beta}=
=\frac{h^{2}\left(2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha+\beta}{2}+2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\right)}{2\sin\alpha\sin\beta}=
=\frac{h^{2}\cos\frac{\alpha+\beta}{2}\left(\sin\frac{\alpha+\beta}{2}+\cos\frac{\alpha-\beta}{2}\right)}{\sin\alpha\sin\beta}=
=\frac{h^{2}\cos\frac{\alpha+\beta}{2}\left(\cos\left(90^{\circ}-\frac{\alpha+\beta}{2}\right)+\cos\frac{\alpha-\beta}{2}\right)}{\sin\alpha\sin\beta}=
=\frac{2h^{2}\cos\frac{\alpha+\beta}{2}\cos\left(45^{\circ}-\frac{\alpha}{2}\right)\cos\left(45^{\circ}-\frac{\beta}{2}\right)}{\sin\alpha\sin\beta}.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1967, № 1, вариант 4

