1441. Остроугольный равнобедренный треугольник и трапеция вписаны в окружность. Одно основание трапеции является диаметром окружности, а боковые стороны параллельны боковым сторонам треугольника. Найдите отношение площадей трапеции и треугольника.
Ответ. 1.
Указание. Выразите площади трапеции и треугольника через радиус окружности и угол при основании равнобедренного треугольника.
Решение. Пусть \alpha
— угол при основании BC
равнобедренного треугольника ABC
, R
— радиус данной окружности, KL
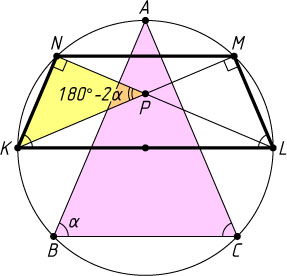
— большее основание равнобедренной трапеции KLMN
, вписанной в окружность. Тогда KL
— диаметр окружности. Поскольку боковые стороны треугольника параллельны боковым сторонам трапеции, то углы при основании трапеции также равны \alpha
, т. е.
\angle NKL=\angle MLK=\angle MLP=\angle ACB=\alpha.
Тогда
KM=NL=2R\sin\angle NKL=2R\sin\alpha,~AB=AC=2R\sin\angle ABC=2R\sin\alpha.
Пусть диагонали KM
и LN
трапеции пересекаются в точке P
. Тогда
\angle KPN=\angle PKL+\angle PLK=2(90^{\circ}-\alpha)=180^{\circ}-2\alpha.
Значит,
S_{KLMN}=\frac{1}{2}KM\cdot NL\sin(180^{\circ}-2\alpha)=\frac{1}{2}\cdot2R\sin\alpha\cdot2R\sin\alpha\sin2\alpha=2R^{2}\sin^{2}\alpha\sin2\alpha,
а так как
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin\angle BAC=R\sin\alpha\cdot2R\sin\alpha\sin2\alpha=2R^{2}\sin^{2}\alpha\sin2\alpha,
то площадь трапеции KLMN
равна площади треугольника ABC
.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 16, с. 200
