1443. Докажите, что четыре точки пересечения окружностей, построенных на сторонах вписанного четырёхугольника как на хордах, и отличные от вершин этого четырёхугольника, лежат на одной окружности.
Указание. Выразите противоположные углы полученного четырёхугольника через углы данного.
Решение. Пусть окружности, построенные на сторонах AB
, BC
, CD
и AD
вписанного четырёхугольника ABCD
как на хордах, пересекаются последовательно в точках K
, L
, M
и N
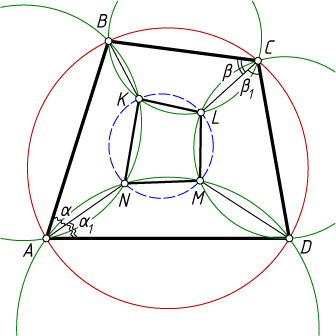
, лежащих внутри этого четырёхугольника и отличных от его вершин. Обозначим
\angle BAN=\alpha,~\angle DAN=\alpha_{1},~\angle BCL=\beta,~\angle DCL=\beta_{1}.
Тогда
\angle NKL=360^{\circ}-\angle BKN-\angle BKL=360^{\circ}-(180^{\circ}-\alpha)-(180^{\circ}-\beta)=\alpha+\beta,
\angle NML=360^{\circ}-\angle DMN-\angle DML=360^{\circ}-(180^{\circ}-\alpha_{1})-(180^{\circ}-\beta_{1})=\alpha_{1}+\beta_{1},
поэтому
\angle NKL+\angle NML=\alpha+\beta+\alpha_{1}+\beta_{1}=
=(\alpha+\alpha_{1})+(\beta+\beta_{1})=\angle BAD+\angle BCD=180^{\circ}.
Следовательно, около четырёхугольника KLMN
можно описать окружность.
