1450. Две окружности пересекаются в точках A
и B
. Прямая, проходящая через точку A
, пересекает окружности в точках M
и N
, отличных от A
, а параллельная ей прямая, проходящая через B
, — соответственно в точках P
и Q
, отличных от B
. Докажите, что MN=PQ
.
Указание. Докажите, что MP\parallel NQ
.
Решение. Поскольку
\angle NQP=\angle NQB=\angle ABQ=\angle BAM=180^{\circ}-\angle BPM=180^{\circ}-\angle MPQ,
то четырёхугольник MNPQ
— параллелограмм. Следовательно, MN=PQ
.
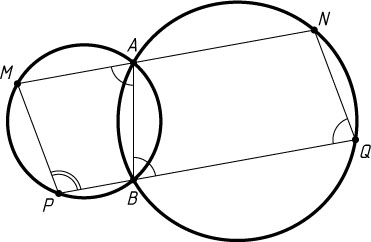
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 63, с. 36
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 92, с. 146
