1451. Рассмотрим все окружности, касающиеся данной прямой и данной окружности (внешним образом). В каждом случае проведём прямую через точки касания. Докажите, что все эти прямые проходят через одну и ту же точку. (Это же верно и для случая внутреннего касания окружностей.)
Указание. Касающиеся окружности гомотетичны относительно их точки касания.
Решение. Касающиеся окружности гомотетичны относительно их точки касания. При гомотетии касательная к одной из окружностей переходит в параллельную ей касательную ко второй, следовательно, все указанные прямые проходят через точку, в которой касательная к данной окружности параллельна данной прямой. Таких точки две. Через одну из них проходят все указанные прямые в случае внешнего касания окружностей, через вторую — в случае внутреннего касания.


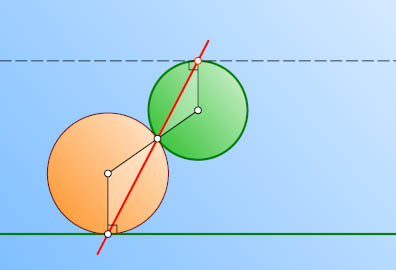
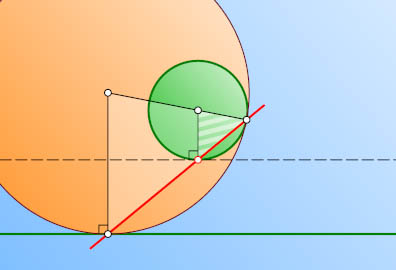
Примечание. Можно доказать, что обоих случаях геометрическое место центров рассматриваемых окружностей — парабола.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 88, с. 38