1466. В остроугольном треугольнике ABC
на высоте AD
взята точка M
, а на высоте BP
— точка N
так, что углы BMC
и ANC
— прямые. Расстояние между точками M
и N
равно 4+2\sqrt{3}
, угол MCN
равен 30^{\circ}
. Найдите биссектрису CL
треугольника CMN
.
Ответ. 7+4\sqrt{3}
.
Указание. Поскольку MD
и NP
— высоты прямоугольных треугольников BMC
и ANC
, проведённые из вершин прямых углов, то
CM^{2}=BC\cdot CD=AC\cdot CP=CN^{2}.
Решение. Из прямоугольных треугольников ACD
и BCP
находим, что
\cos\angle ACB=\frac{CD}{AC}=\frac{CP}{BC},
откуда BC\cdot CD=CP\cdot AC
.
Поскольку MD
и NP
— высоты прямоугольных треугольников BMC
и ANC
, проведённые из вершин прямых углов, то
CM^{2}=BC\cdot CD=AC\cdot CP=CN^{2},
поэтому CM=CN
.
Биссектриса CL
равнобедренного треугольника CMN
является его высотой и медианой, следовательно
CL=ML\ctg\angle MCL=\frac{1}{2}MN\ctg15^{\circ}=
=\frac{(2+\sqrt{3})(1+\cos30^{\circ})}{\sin30^{\circ}}=(2+\sqrt{3})^{2}=7+4\sqrt{3}.
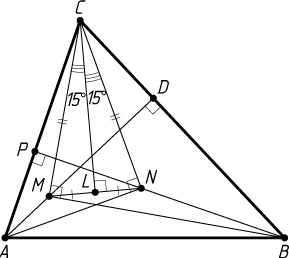
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1994 (предварительный экзамен), № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.44, с. 140
