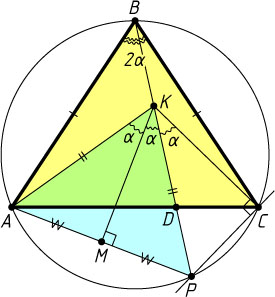
1467. На основании AC
равнобедренного треугольника ABC
взята точка D
, а на отрезке BD
— точка K
, причём AD:DC=\angle AKD:\angle DKC=2:1
. Докажите, что \angle AKD=\angle ABC
.
Решение. Обозначим \angle DKC=\alpha
, \angle AKD=2\alpha
. Поскольку площадь треугольника AKD
вдвое больше площади треугольника DKC
, то
AK\cdot KD\sin2\alpha=2CK\cdot KD\sin\alpha,
откуда находим, что AK=\frac{CK}{\cos\alpha}
.
Через точку C
проведём прямую, перпендикулярную прямой KC
, до пересечения с продолжением BD
в точке P
. Из прямоугольного треугольника KCP
находим, что KP=\frac{CK}{\cos\alpha}=AK
. Следовательно, треугольник AKP
— равнобедренный.
Пусть KM
— высота этого треугольника. Тогда \angle MKP=\alpha
. Из равенства прямоугольных треугольников KMP
и KCP
(по гипотенузе и острому углу) следует, что \angle APB=\angle CPB
.
Из треугольников ABP
и CBP
по теореме синусов находим, что
\frac{BP}{\sin\angle BAP}=\frac{AB}{\sin\angle APB}=\frac{BC}{\sin\angle CPB}=\frac{BP}{\sin\angle BCP},
откуда \sin\angle BAP=\sin\angle BCP
, а так как углы BAP
и BCP
различны, то их сумма равна 180^{\circ}
. Значит, четырёхугольник ABCP
— вписанный. Следовательно,
\angle ABC=180^{\circ}-\angle APC=180^{\circ}-2(90^{\circ}-\alpha)=2\alpha=\angle AKD.
Автор: Шарыгин И. Ф.
Источник: Журнал «Crux Mathematicorum». — 1990, № 6, задача 1436 (1989, с. 110), с. 186; 1990, № 9, задача 178 (1459), с. 280
Источник: Соросовская олимпиада. — 1994, I, III тур, 2-й раунд, 11 класс
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 971, с. 119
