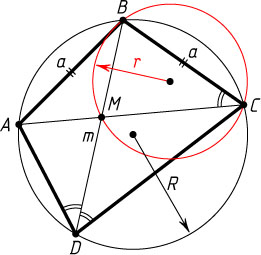
1470. Диагонали вписанного в окружность радиуса R
четырёхугольника ABCD
пересекаются в точке M
. Известно, что AB=BC=a
, BD=m
. Найдите радиус окружности, описанной около треугольника BCM
.
Ответ. \frac{aR}{m}
.
Указание. Треугольники BCM
и BDC
подобны.
Решение. Вписанные углы BDC
и BDA
опираются на равные дуги, поэтому они равны. Тогда \angle BCM=\angle BCA=\angle BDC
.
Треугольники BCM
и BDC
подобны по двум углам (угол при вершине B
— общий), причём коэффициент подобия k
равен \frac{BC}{BD}=\frac{a}{m}
. Пусть r
— радиус окружности, описанной около треугольника BCM
. Тогда
r=kR=\frac{a}{m}\cdot R=\frac{aR}{m}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 918, с. 113
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.38, с. 139
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 14.38.1, с. 150
