1473. Докажите, что проекции вершины треугольника на четыре биссектрисы внешних и внутренних углов при двух других вершинах лежат на одной прямой.
Указание. Пусть D
— проекция вершины A
треугольника ABC
на биссектрису внешнего угла при вершине B
. Продолжите отрезок AD
до пересечения с прямой BC
в точке K
. Тогда D
— середина отрезка AK
.
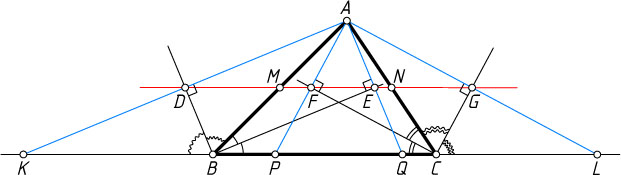
Решение. Пусть E
и D
— проекции вершины A
треугольника ABC
на биссектрисы соответственно внутреннего и внешнего углов при вершине B
, а точки F
и G
— проекции вершины A
на биссектрисы соответственно внутреннего и внешнего углов при вершине C
, M
и N
— середины сторон AB
и AC
соответственно.
Продолжим отрезок AD
до пересечения с прямой BC
в точке K
. В треугольнике ABK
биссектриса BD
является высотой, поэтому треугольник ABK
равнобедренный. Значит, BD
— его медиана, а точка D
— середина отрезка AK
. Поэтому DM
— средняя линия треугольника ABK
, значит, DM\parallel BC
.
Аналогично докажем, что EM\parallel BC
, GN\parallel BC
и FN\parallel BC
, а так как MN
— средняя линия треугольника ABC
, то MN\parallel BC
. Следовательно, точки E
, D
, F
и G
лежат на прямой MN
. Что и требовалось доказать.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 6
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.54, с. 107
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.47, с. 110
