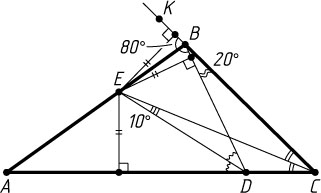
1476. В треугольнике ABC
угол B
равен 100^{\circ}
. В этом треугольнике проведена биссектриса угла C
, пересекающая сторону AB
в точке E
, а на стороне AC
взята точка D
так, что угол CBD
равен 20^{\circ}
. Докажите, что угол CED
равен 10^{\circ}
.
Указание. Если K
— точка на продолжении стороны BC
за точку B
, то BA
— биссектриса угла DBK
.
Решение. На продолжении стороны BC
за точку B
отметим точку K
. Тогда
\angle ABK=180^{\circ}-\angle ABC=180^{\circ}-100^{\circ}=80^{\circ},
а так как
\angle ABD=\angle ABC-\angle DBC=100^{\circ}-20^{\circ}=80^{\circ},
то луч BA
— биссектриса угла KBD
. Точка E
, лежащая на этой биссектрисе, равноудалена от сторон угла KBD
, а так как CE
— биссектриса угла ACB
, то точка E
равноудалена и от сторон угла ACB
. Значит, точка E
равноудалена от сторон угла ADB
, следовательно, DE
— биссектриса угла ADB
.
По теореме о внешнем угле треугольника
\angle ADB=\angle CBD+\angle ACB=20^{\circ}+\angle ACB,~\angle ADE=\angle CED+\angle ACE.
Следовательно,
\angle CED=\angle ADE-\angle ACE=\frac{1}{2}\angle ADB-\frac{1}{2}\angle ACB=
=\frac{1}{2}(20^{\circ}+\angle ACB)-\angle ACE=(10^{\circ}+\angle ACE)-\angle ACE=10^{\circ}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 729, с. 92
