1480. Дана окружность радиуса R
с центром O
. Две другие окружности касаются данной изнутри и пересекаются в точках A
и B
. Найдите сумму радиусов двух последних окружностей, если известно, что \angle OAB=90^{\circ}
.
Ответ. R
.
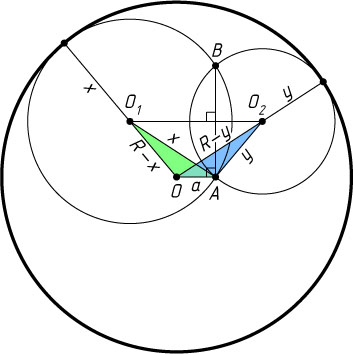
Решение. Пусть O_{1}
— центр окружности радиуса x
, O_{2}
— центр окружности радиуса y
. Эти окружности касаются изнутри данной окружности, поэтому OO_{1}=R-x
и OO_{2}=R-y
.
Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде, поэтому O_{1}O_{2}\perp AB
, а так как OA\perp AB
, то O_{1}O_{2}\parallel OA
. Следовательно, треугольники OAO_{1}
и OAO_{2}
равновелики.
Пусть OA=a
, а p_{1}
и p_{2}
— полупериметры треугольников OAO_{1}
и OAO_{2}
соответственно. Тогда
p_{1}=\frac{x+R-x+a}{2}=\frac{R+a}{2},~p_{2}=\frac{y+R-y+a}{2}=\frac{R+a}{2}.
По формуле Герона
S^{2}_{\triangle OAO_{1}}=p_{1}(p_{1}-AO_{1})(p_{1}-OO_{1})(p_{1}-OA)=
=\frac{R+a}{2}\left(\frac{R+a}{2}-x\right)\left(\frac{R+a}{2}-R+x\right)\left(\frac{R+a}{2}-a\right)=
=\frac{(R^{2}-a^{2})(a^{2}-(R-2x)^{2})}{16}.
Аналогично
S^{2}_{\triangle OAO_{2}}=\frac{(R^{2}-a^{2})(a^{2}-(R-2y)^{2})}{16},
а так как S_{\triangle OAO_{1}}=S_{\triangle OAO_{2}}
, то (R-2x)^{2}=(R-2y)^{2}
, или (y-x)(R-x-y)=0
. Заметим, что x\ne y
, так как в противном случае точки O
, A
и B
лежали бы на одной прямой. Значит, R-x-y=0
. Следовательно, x+y=R
.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 266, с. 30
