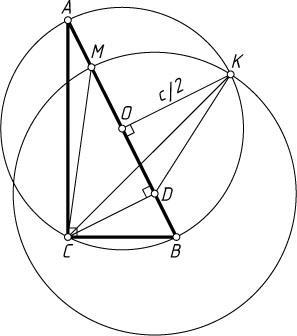
1481. Около прямоугольного треугольника ABC
(\angle C=90^{\circ}
) описана окружность. Пусть CD
— высота треугольника. Окружность с центром D
проходит через середину дуги AB
и пересекает AB
в точке M
. Найдите CM
, если AB=c
.
Ответ. \frac{c}{\sqrt{2}}
.
Решение. Пусть O
— центр окружности, R=\frac{c}{2}
— её радиус, K
— середина дуги, не содержащей точки C
, AD\gt AO
. Тогда
CM^{2}=CD^{2}+DM^{2}=BD\cdot AD+DK^{2}=(R-OD)(R+OD)+OK^{2}+OD^{2}=
=R^{2}-OD^{2}+R^{2}OD^{2}=2R^{2}.
Следовательно,
CM=R\sqrt{2}=\frac{c}{2}\cdot\sqrt{2}=\frac{c}{\sqrt{2}}.
Аналогично для случая, когда точка K
— середина дуги ACB
.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 262, с. 30
