1482. Дан равнобедренный треугольник ABC
с основанием AC
, AD
— его биссектриса. Перпендикуляр, восставленный к AD
в точке D
, пересекает продолжение AC
в точке E
. Основания перпендикуляров, опущенных из точек B
и D
на AC
, — M
и N
соответственно. Найдите MN
, если AE=a
.
Ответ. \frac{a}{4}
.
Решение. Пусть прямые DE
и AB
пересекаются в точке P
. Через точку D
проведём прямую, параллельную AC
. Пусть K
— точка пересечения этой прямой со стороной AB
. Тогда
\angle ADK=\angle CAD=\angle DAK,
значит, треугольник AKD
равнобедренный, AK=KD
. Точка K
лежит на серединном перпендикуляре к катету AD
прямоугольного треугольника ADP
, значит, K
— середина гипотенузы AP
этого треугольника. В то же время, DK
— средняя линия треугольника APE
, поэтому DK=\frac{1}{2}AE=\frac{1}{2}a
.
Пусть Q
— точка пересечения DK
и BM
. Тогда MQDN
— прямоугольник, следовательно,
MN=DQ=\frac{1}{2}DK=\frac{1}{2}\cdot\frac{1}{2}a=\frac{1}{4}a.
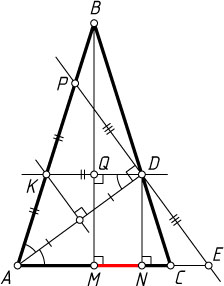
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 289, с. 33
