1485. AD
— биссектриса треугольника ABC
, l
— касательная, проведённая в точке A
к описанной окружности треугольника ABC
. Докажите, что прямая, проходящая через точку D
параллельно l
, касается вписанной окружности треугольника.
Решение. Обозначим \angle BAC=\alpha
, \angle ACB=\gamma
. При симметрии относительно AD
прямая BC
переходит в касательную к вписанной окружности треугольника ABC
, проходящую через точку D
, а точка B
— в точку E
, лежащую на прямой AC
. Тогда
\angle ADE=\angle ADB=\angle ACD+\angle DAC=\gamma+\frac{\alpha}{2}.
Пусть F
— точка прямой l
, причём F
и C
лежат по разные стороны от прямой AD
. Из теоремы об угле между касательной и хордой следует, что \angle BAF=\angle ACB=\gamma
, поэтому
\angle DAF=\angle DAB+\angle BAF=\gamma+\frac{\alpha}{2}.
Из равенства углов ADE
и DAF
следует параллельность прямых DE
и l
. Через точку D
проходит единственная прямая, параллельная прямой l
, значит, прямая DE
, проходящая через точку D
параллельно l
, касается вписанной окружности треугольника ABC
. Что и требовалось доказать.
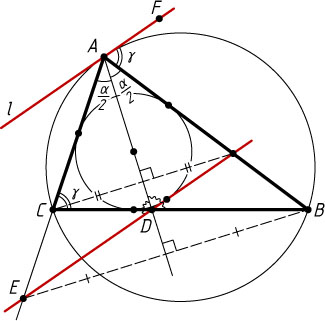
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 413, с. 49
