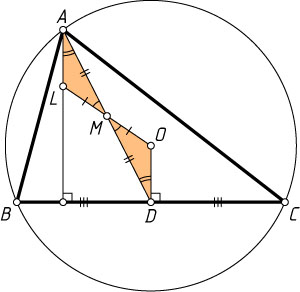
1492. Докажите, что точки, симметричные центру описанной около треугольника окружности относительно середин медиан, лежат на высотах треугольника (или на их продолжениях).
Решение. Пусть O
— центр описанной окружности треугольника ABC
, L
— точка, симметричная точке O
относительно середины M
медианы AD
.
Треугольники AML
и DMO
равны по двум сторонам и углу между ними, поэтому \angle MAL=\angle MDO
, значит, AL\parallel OD
, а так как OD
— серединный перпендикуляр к отрезку BC
, то AL\perp BC
. Следовательно, точка L
лежит на высоте треугольника ABC
, опущенной на сторону BC
(или на продолжении этой высоты).
Аналогично для точек, симметричных центру O
относительно середин двух других медиан.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 415, с. 50
